પ્રમાણભૂત વિચલન

સંભાવના અને આંકડામાં, રેન્ડમ ચલનું પ્રમાણભૂત વિચલન એ સરેરાશ મૂલ્યથી રેન્ડમ ચલનું સરેરાશ અંતર છે.

તે રજૂ કરે છે કે કેવી રીતે સરેરાશ મૂલ્યની નજીક રેન્ડમ ચલનું વિતરણ થાય છે. નાના પ્રમાણભૂત વિચલન સૂચવે છે કે રેન્ડમ ચલ સરેરાશ મૂલ્યની નજીક વહેંચવામાં આવે છે. મોટા પ્રમાણભૂત વિચલન સૂચવે છે કે રેન્ડમ ચલ સરેરાશ મૂલ્યથી દૂર વહેંચાયેલું છે.

માનક વિચલન વ્યાખ્યા સૂત્ર

પ્રમાણભૂત વિચલન એ rand ની સરેરાશ કિંમત સાથે, રેન્ડમ ચલ X ના ભિન્નતાનો વર્ગમૂળ છે.

$ig સિગ્મા = એસટીડી (એક્સ) = \ ચોરસ {વર (એક્સ)} = \ ચોરસ t ઇ ((એક્સ- \ મ્યુ) ^ 2$

આપણે મેળવી શકીએ છીએ તે પ્રમાણભૂત વિચલનની વ્યાખ્યામાંથી

$\ સિગ્મા = એસટીડી (એક્સ) = \ ચોરસ {ઇ (એક્સ ^ 2) - \ મ્યુ ^ 2}$

સતત રેન્ડમ ચલનું માનક વિચલન

સરેરાશ મૂલ્ય with અને સંભાવના ઘનતા ફંક્શન એફ (એક્સ) સાથે સતત રેન્ડમ ચલ માટે:

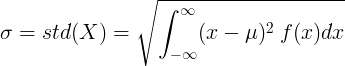
$ig સિગ્મા = એસટીડી (એક્સ) = \ ચોરસ t \ અંત _ _ - \ ઇન્ફ્ટી} {{\ ઇન્ફ્ટી x (એક્સ- \ મ્યુ) ^ 2 \: એફ (એક્સ) ડીએક્સ}$

અથવા

$\ સિગ્મા = એસટીડી (એક્સ) = \ ચોરસ {\ બાકી [\ પૂર્ણાંક _ {- ty ઇન્ફ્ટી ^ ^ {\ ઇન્ફ્ટી} x ^ 2 \: એફ (એક્સ) ડીએક્સ \ અધિકાર] - \ મ્યુ ^ 2}$

સ્વતંત્ર રેન્ડમ ચલનું માનક વિચલન

સરેરાશ મૂલ્ય with અને સંભવિત માસ ફંક્શન પી (x) સાથેના સ્વતંત્ર રેન્ડમ ચલ X માટે:

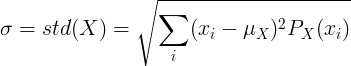
$ig સિગ્મા = એસટીડી (એક્સ) = \ ચોરસ t \ સમ_ {હું {} {} (x_i- \ mu _X) ^ 2P_X (x_i)}$

અથવા

$\ સિગ્મા = એસટીડી (એક્સ) = \ ચોરસ {\ ડાબી [\ રકમ_ {i} ^ {_ x_i ^ 2 પી (x_i) \ અધિકાર] - \ મૂ ^ 2}$

સંભાવના વિતરણ ►

પ્રમાણભૂત વિચલન

માનક વિચલન વ્યાખ્યા સૂત્ર

સતત રેન્ડમ ચલનું માનક વિચલન

સ્વતંત્ર રેન્ડમ ચલનું માનક વિચલન

આ પણ જુઓ

સંભાવના અને આંકડા