Lárnach

Is é atá sa chomhtháthú ná oibriú droim ar ais an díorthaithe.

Is é comhthreomhar feidhme an limistéar faoi ghraf na feidhme.

Sainmhíniú Comhtháite Éiginnte

Cathain dF (x) / dx = f (x) =/ dhílis (f (x) * dx) = F (x) + c

Airíonna Comhtháite Éiginnte

dhílis (f (x) + g (x)) * dx = gné dhílis (f (x) * dx) + lárnach (g (x) * dx)

dhílis (a * f (x) * dx) = a * dhílis (f (x) * dx)

dhílis (f (a * x) * dx) = 1 / a * F (a * x) + c

dhílis (f (x + b) * dx) = F (x + b) + c

dhílis (f (a * x + b) * dx) = 1 / a * F (a * x + b) + c

dhílis (df (x) / dx * dx) = f (x)

Athrú ar Chomhtháthú Inathraithe

Cathainx = g (t) agusdx = g '(t) * dt

dhílis (f (x) * dx) = dhílis (f (g (t)) * g '(t) * dt)

Comhtháthú De réir Páirteanna

dhílis (f (x) * g '(x) * dx) = f (x) * g (x) - lárnach (f' (x) * g (x) * dx)

Tábla Comhtháthaithe

dhílis (f (x) * dx = F (x) + c

dhílis (a * dx) = a * x + c

slánuimhir (x ^ n * dx) = 1 / (a ​​+ 1) * x ^ (a + 1) + c, nuair a </ - 1

dhílis (1 / x * dx) = ln (abs (x)) + c

dhílis (e ^ x * dx) = e ^ x + c

dhílis (a ^ x * dx) = a ^ x / ln (x) + c

dhílis (ln (x) * dx) = x * ln (x) - x + c

dhílis (sin (x) * dx) = -cos (x) + c

dhílis (cos (x) * dx) = sin (x) + c

dhílis (tan (x) * dx) = -ln (abs (cos (x))) + c

dhílis (arcsin (x) * dx) = x * arcsin (x) + sqrt (1-x ^ 2) + c

dhílis (arccos (x) * dx) = x * arccos (x) - sqrt (1-x ^ 2) + c

dhílis (arctan (x) * dx) = x * arctan (x) - 1/2 * ln (1 + x ^ 2) + c

dhílis (dx / (ax + b)) = 1 / a * ln (abs (a * x + b)) + c

dhílis (1 / sqrt (a ^ 2-x ^ 2) * dx) = arcsin (x / a) + c

dhílis (1 / sqrt (x ^ 2 + - a ^ 2) * dx) = ln (abs (x + sqrt (x ^ 2 + - a ^ 2)) + c

dhílis (x * sqrt (x ^ 2-a ^ 2) * dx) = 1 / (a ​​* arccos (x / a)) + c

dhílis (1 / (a ​​^ 2 + x ^ 2) * dx) = 1 / a * arctan (x / a) + c

dhílis (1 / (a ​​^ 2-x ^ 2) * dx) = 1 / 2a * ln (abs (((a + x) / (ax))) + c

dhílis (sinh (x) * dx) = cosh (x) + c

dhílis (cosh (x) * dx) = sinh (x) + c

dhílis (tanh (x) * dx) = ln (cosh (x)) + c

 

Sainmhíniú Comhtháite Cinnte

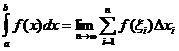
dhílis (a..b, f (x) * dx) = lim (n-/ inf, suim (i = 1..n, f (z (i)) * dx (i))) 

Cathainx0 = a, xn = b

dx (k) = x (k) - x (k-1)

x (k-1) <= z (k) <= x (k)

Ríomh Comhtháite Cinnte

Cathain ,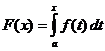

 dF (x) / dx = f (x) agus

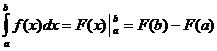
dhílis (a..b, f (x) * dx) = F (b) - F (a) 

Airíonna Comhtháite Cinnte

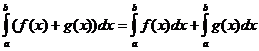
slánuimhir (a..b, (f (x) + g (x)) * dx) = dhílis (a..b, f (x) * dx) + lárnach (a..b, g (x) * dx )

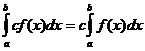
dhílis (a..b, c * f (x) * dx) = c * dhílis (a..b, f (x) * dx)

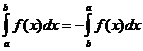
dhílis (a..b, f (x) * dx) = - gné dhílis (b..a, f (x) * dx)

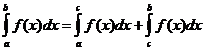
dhílis (a..b, f (x) * dx) = dhílis (a..c, f (x) * dx) + dhílis (c..b, f (x) * dx)

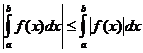
abs (dhílis (a..b, f (x) * dx)) <= dhílis (a..b, abs (f (x)) * dx)

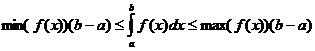min (f (x)) * (ba) <= dhílis (a..b, f (x) * dx) <= uas (f (x)) * (ba) Cathainx ball de [a, b]

Athrú ar Chomhtháthú Inathraithe

Cathainx = g (t) ,dx = g '(t) * dt ,g (alfa) = a ,g (béite) = b

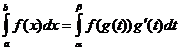
dhílis (a..b, f (x) * dx) = dhílis (alfa..beta, f (g (t)) * g '(t) * dt)

Comhtháthú De réir Páirteanna

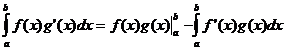
dhílis (a..b, f (x) * g '(x) * dx) = dhílis (a..b, f (x) * g (x) * dx) - lárnach (a..b, f' (x) * g (x) * dx)

Teoirim meánluacha

Nuair a bhíonn f ( x ) leanúnach tá pointe anntá c ina bhall de [a, b] mar sin

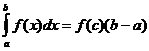
dhílis (a..b, f (x) * dx) = f (c) * (ba)  

Comhfhogasú traipéisóideach ar Integral Cinnte

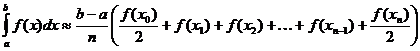
dhílis (a..b, f (x) * dx) ~ (ba) / n * (f (x (0)) / 2 + f (x (1)) + f (x (2)) + .. . + f (x (n-1)) + f (x (n)) / 2)

Feidhm na Gáma

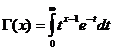
gáma (x) = lárnach (0..inf, t ^ (x-1) * e ^ (- t) * dt

Tá an fheidhm gáma cóineasaithe do x/ 0 .

Airíonna Feidhm Gáma

G ( x +1) = x G ( x )

G ( n +1) = n ! , nuair n nℕ (slánuimhir dearfach).ina bhall de

Feidhm na Béite

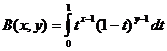
B (x, y) = dhílis (0..1, t ^ (n-1) * (1-t) ^ (y-1) * dt

Feidhm Béite agus Gaol Feidhme Gáma

B (x, y) = Gáma (x) * Gáma (y) / Gáma (x + y)

 

Advertising

 

 

CALCULUS